Soal UN Matematika SMA beserta pembahasan

1. Sebuah kapal berlayar kearah timur sejauh 30 mil Kemudian melanjutkan perjalanan dengan arah 030° sejauh 60 mil. Jarak kapal terhadap posisi saat kapal berangkat adalah … mil.

A. 10

B. 30

C. 30

D. 30

E. 30

PEMBAHASAN :

Mengingat arah mata angin maka arah timur membentuk sudut 0900 dari arah utara. Dengan memperhatikan soal sebelumnya maka sudut apit yang dibentuk adalah 120°.

Misal titi awalnya adalah A dan panjang lintasan kearah timur adalah AB = 30km dan panjang lintasan selanjutnya adalah BC = 60km.

AC2 = AB2 + BC2 – 2(AB)(BC)cos ACB

= 302 + 602 – 2(30)(60)cos 1200

= 900 + 3600 – 3600()

= 4500 + 1800

= 6300

= 7 x 9 x 100

AC = 30

JAWABAN : B

2. Nilai sinus sudut terkecil dari segitiga yang sisinya 5 cm, 6 cm, cm adalah …

A. 1/5 

B. 1/6 

C. 1/5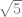 

D. 1/6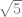 

E. 1/3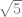 

PEMBAHASAN :

Perhatikan soal nomer.5 diatas, dilihat dari perhitungan tersebut, maka sudut yang memiliki nilai sin yang terkecil adalah sudut yang didepannya memiliki panjang sisi terpendek.

Misal AB = 5cm = cm, BC = 6cm = cm dan AC = cm

Dari panjang ketiga sisi tersebut, panjang sisi terpendek adalah sisi AC. Jadi sudut yang dimaksud adalah ABC

Pandang sudut ABC :

AC2 = AB2 + BC2 – 2(AB)(BC)cos ABC

()2 = 52 + 62 – 2(5)(6)cos b

21 = 25 + 36 – 2(5)(6) cos b

40 = 2(5)(6) cos b

2/3 = cos b

sin b = 

= 

= 

= 1/3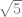 

JAWABAN : E

3. Luas segitiga ABC adalah (3 + 2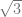) cm. Jika panjang sisi AB = (6 + 4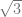) cm dan BC = 7 cm, maka nilai sin(A + C) = …

1. A. 6
   B. 3
   C. 1/7
   D. 
   E. 
   PEMBAHASAN :
   misal AB = c dan BC = a dan sudut apitnya adalah B
   Luas ABC = .a.c.sin B
   3 + 2 = .7. (6 + 4) sin B
   3 + 2 = .7. 2(3 + 2) sin B
   3 + 2 = 7(3 + 2) sin B
   1 = 7 sin B
   1/7 = sin B
   sin (A + C) = sin(1800 – B)
   = sin B
   = 1/7
   JAWABAN : C

4. Diketahui A dan B adalah titik–titik ujung sebuah terowongan yang dilihat dari C dengan sudut ACB = 45°. Jika jarak CB = p meter dan CA = 2p meter, maka panjang terowongan itu adalah … meter.

1. A. p
   B. p
   C. 3
   D. 4p
   E. 5p
   PEMBAHASAN :
   Dalam kasus soal ini kita akan memanfaatkan aturan kosinus :
   Rumus aturan kosinus adalah kuadrat sisi depan sudut = jumlah kuadrat sisi yang mengapit sudut dikurangi 2 cos sudut apit.
   AB2 = CA2 + CB2 – 2(CA)(CB)cos ACB
   = (2p)2 + (p)2 – 2(2p)(p)cos 450
   = 8p2 + p2 – (4p2)()
   = 9p2 – (4p2)()
   = 9p2 – 4p2 
   = 5p2
   AB = p
   JAWABAN : A

5. Sebuah kapal berlayar dari pelabuhan A dengan arah 044° sejauh 50 km. Kemudian berlayar lagi dengan arah 104° sejauh 40 km ke pelabuhan C Jarak pelabuhan A ke C adalah … km.

1. A. 10
   B. 10
   C. 10
   D. 10
   E. 10
   PEMBAHASAN :
   Perlu diingat bahwa sudut yang dibentuk dalam soal tersebut dihitung dari arah utara. Jadi 044° dari arah utara dan 104° dari arah utara juga. (INGAT : jurusan tiga angka).
   Panjang AB = 50km dan panjang BC = 40km.
   Kemudian kita penyelesaian soal ini menggunakan aturan kosinus dengan sudut apit yang dibentuk atau ABC adalah 120°(maaf belum bisa bikin gambarnya)
   AC2 = AB2 + BC2 – 2(AB)(BC)cos ACB
   = 502 + 402 – 2(50)(40)cos 1200
   = 2500 + 1600 – 4000()
   = 4100 + 2000
   = 6100
   = 61 x 100
   AC = 10
   JAWABAN : E